Quantum Information Theory
We explore various aspects of quantum information theory, with implications for both our fundamental understanding of the laws of quantum physics and their technological uses.
Approximate Markov Chains
Quantum Markov chains are multipartite quantum states that can be generated from consecutive local interactions. They are characterized by the property that the conditional mutual information (CMI), an entropic quantity, vanishes. We study states that have a CMI that is non-zero but small, the so-called approximate quantum Markov chains [1]. These states still obey the property that they can be approximately generated from consecutive local interactions. This feature enables us to connect the concepts of Markov chains with the theory of quantum error correction. More precisely, if we lose part of a multipartite state that has the approximate Markov structure, we can reconstruct the lost system with a recovery map that acts only locally on a small system [2].
References
- Omar Fawzi and Renato Renner. Quantum conditional mutual information and approximate Markov chains. Comm. Math. Phys. 340, 575 (2015). external page doi: 10.1007/s00220-015-2466-x
- David Sutter, Omar Fawzi and Renato Renner. Universal recovery map for approximate Markov chains. Proc. R. Soc. Lond. 472, 2186 (2016). external page doi: 10.1098/rspa.2015.0623
Further reading
- Marius Junge, Renato Renner, David Sutter, Mark M. Wilde and Andreas Winter. Universal recovery maps and approximate sufficiency of quantum relative entropy. Ann. Henri Poincaré 19, 2955 (2018). external page doi: 10.1007/s00023-018-0716-0
- David Sutter, Mario Berta and Marco Tomamichel. Multivariate trace inequalities. Comm. Math. Phys. 352, 37 (2017). external page doi: 10.1007/s00220-016-2778-5
- David Sutter. Approximate quantum Markov chains. In: Approximate Quantum Markov Chains. SpringerBriefs in Mathematical Physics, vol. 28 (2018). external page doi: 10.1007/978-3-319-78732-9_5 external page arxiv:1802.05477
Symmetry in Quantum Information
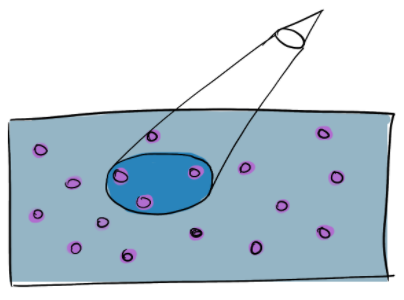
Systems with permutation symmetry are prevalent in physics. In practical scenarios of quantum information, for instance, we frequently deal with multipartite quantum states that are invariant under permutations. These states can have complex structures that are hard to deal with due to quantum correlations between the parties. Luckily, symmetry can lead to independence [1]. An important direction in our research is the study and development of tools to harness symmetry in quantum information, to efficiently tackle the complexity. A representative example of such tools is the quantum de Finetti theorem [2], which tells us that one part of a symmetric state can be treated as a mixture of identically prepared quantum states that have no correlation between the parties. Following these seminal works, we seek to refine and extent the quantum de Finetti theorem and to apply it to various fields including cryptography, metrology, computation, and communication. We also developed optimal compression protocols for identically prepared quantum states [3]. Combined with the quantum de Finetti theorem, such protocols enable efficient storage of a broad range of quantum states.
References
- Renato Renner. Symmetry of large physical systems implies independence of subsystems. Nat. Phys. 3, 645 (2007). external page doi: 10.1038/nphys684 external page arxiv:quant-ph/0703069
- Matthias Christandl, Robert Koenig, Graeme Mitchison and Renato Renner. One-and-a-half quantum de Finetti theorems. Comm. Math. Phys. 273, 473 (2007). external page doi: 10.1007/s00220-007-0189-3 external page arxiv:quant-ph/0602130
- Yuxiang Yang, Ge Bai, Giulio Chiribella, Masahito Hayashi. Compression for quantum population coding. IEEE Trans. Inf. Theory 64, 4766 (2018). external page doi:10.1109/TIT.2017.2788407 external page arxiv:1701.03372
Further reading
- Matthias Christandl, Robert König and Renato Renner. Postselection technique for quantum channels with applications to quantum cryptography. Phys. Rev. Lett. 102, 020504 (2009) external page doi: 10.1103/PhysRevLett.102.020504 external page arxiv:0809.3019
- Yuxiang Yang, Giulio Chiribella, and Masahito Hayashi. Optimal compression for identically prepared qubit states. Phys. Rev. Lett. 117, 090502 (2016). external page doi: 10.1103/PhysRevLett.117.090502 external page arxiv:1606.02893
Entropy Accumulation
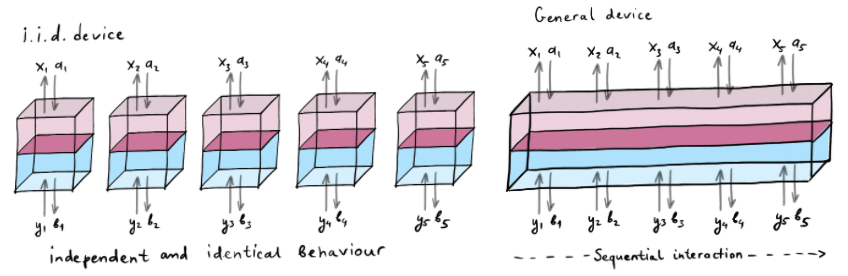
One major difficulty in proving the security of cryptographic protocols is the fact that an adversary could utilize complicated strategies to attack the scheme. The so-called i.i.d. (independent and identically distributed) strategies, where it is assumed that the attacking strategy for the eavesdropper is the same for each round of the protocol, are usually relatively simple to analyze. However, this does obviously not capture the full power of all possible attacking strategies. A technical tool from information theory we developed is Entropy Accumulation Theorem (EAT) [1], which allows us to reduce arbitrary strategies to i.i.d. strategies. In turn, this tool enables simple device-independent security proofs [2].
The EAT ensures that the operationally relevant quantities of a multiparty system (the smooth min-and max-entropies) can be bounded by the sum of the von Neumann entropies of its individual parts viewed in a worst-case scenario. Current research efforts aim to generalize this result and applying it to areas beyond quantum cryptography.
References
- Frederic Dupuis, Omar Fawzi and Renato Renner. Entropy accumulation. Commun. Math. Phys. 379, 867 (2020). external page doi: 10.1007/s00220-020-03839-5
- Rotem Arnon-Friedman, Renato Renner and Thomas Vidick. Simple and tight device-independent security proofs. SIAM J. Comput. 48, 181 (2019). external page doi: 10.1137/18M1174726
Further reading
- Rotem Arnon-Friedman, Frédéric Dupuis, Omar Fawzi, Renato Renner and Thomas Vidick. Practical device-independent quantum cryptography via entropy accumulation. Nat. Commun. 9, 459 (2018). external page doi: 10.1038/s41467-017-02307-4
- Rotem Arnon-Friedman. Reductions to IID in device-independent quantum information processing. external page arxiv:1812.10922
Quantum Tomography
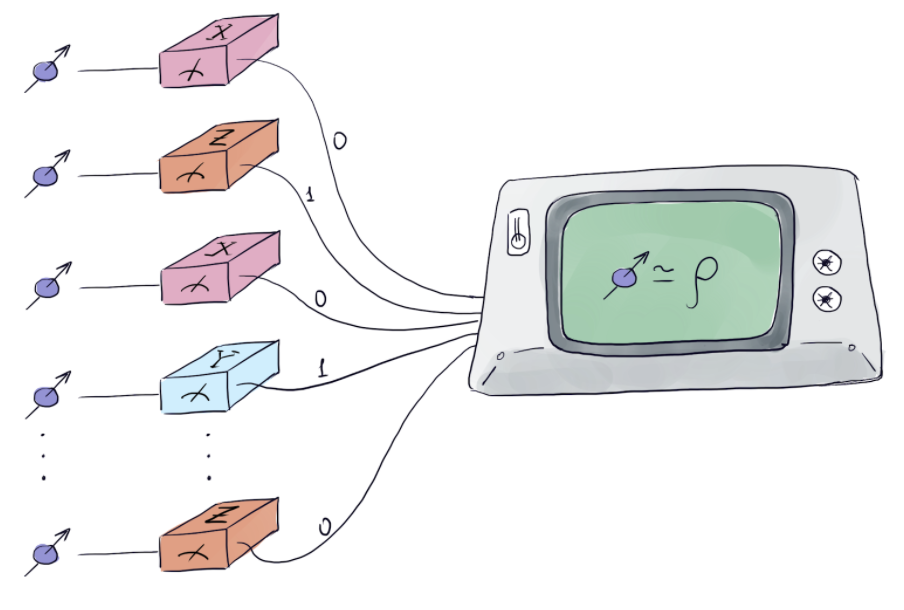
Quantum state tomography is the task of estimating an unknown quantum state from some measurement data, which is an essential element of current research in quantum information processing. Theoretically, it amounts to constructing an estimator using only the data from measurements on a finite number of copies of a state. Many estimators have been proposed, but the error analysis is often ignored or not treated rigorously. We have developed a reliable and practical scheme for quantum state tomography [1], based on a post-selection technique from studying the quantum de Finetti property of a permutation-invariant sample of states. A ready-to-use software package has been developed to implement the scheme [2]. Alternatively, by extending classical statistical methods to the quantum setting, we proposed a different scheme that significantly improves the error estimates of the previous method [3].
References
- Matthias Christandl and Renato Renner. Reliable quantum state tomography. Phys. Rev. Lett. 109, 120403 (2012). external page doi: 10.1103/PhysRevLett.109.120403 external page arxiv:1108.5329
- Philippe Faist and Renato Renner. Practical, reliable error bars in quantum tomography. Phys. Rev. Lett. 117, 010404 (2016). external page doi: 10.1103/PhysRevLett.117.010404 external page arxiv:1509.06763
- Jinzhao Wang, Volkher B. Scholz and Renato Renner. Confidence polytopes in quantum state tomography. Phys. Rev. Lett. 122, 190401 (2019). external page doi: 10.1103/PhysRevLett.122.190401 external page arxiv:1808.09988
Quantum information processing and uncertainty relations
Quantum information processing is constrained by the uncertainty principle. For instance, arbitrary information cannot be copied. Otherwise, it would be possible to accurately measure non-commuting observables such as position and momentum. This has implications for quantum error-correction and quantum cryptography, among many others. We study the possibilities of and limits on information processing protocols and how these are connected to uncertainty relations.
Our research also involves developing new ways to bound the performance of information processing protocols. For example, we have formulated a bound on the performance of quantum error-correcting codes in terms of a semidefinite program [1], and more recently extended this technique to find tight bounds on the performance of quantum data compression [2]. We have also recently discovered that the entropic uncertainty relation implies a duality between pairs of quantum channels, so that the performance of one channel (for instance, its ability to transmit information) very tightly constrains the performance of the other [3].
This partly entails developing new uncertainty relations. An important contribution in this area is the realization that entanglement enables to circumventing the usual formulation of the uncertainty principle. This subtle effect is revealed by uncertainty relations formulated in terms of entropy [4, 5]. This entropic approach has subsequently led to much simpler security proofs of quantum cryptographic protocols than those known previously. More recently we have formulated error–disturbance tradeoffs for quantities that are more directly operationally relevant, which for instance implies that wave–duality relations can be understood as error-disturbance uncertainty relations [6].
Finally, we construct new information-processing protocols with improved performance. Here the connection to the uncertainty principle enables us to convert high-performance classical protocols to high-performance quantum protocols. The best example is our construction of quantum polar codes from classical polar codes [7]. The latter are the first discovered class of error-correcting codes that can achieve the capacity of any classical channel using efficient encoding and decoding operations. Their quantum counterpart remains the only explicitly known code family that can achieve the coherent information of arbitrary channels, and brought efficient encoding and decoding operations for high-rate codes into the quantum realm for the first time. The connection to classical codes via the uncertainty principle also leads to insight into the structure of classical polar codes [8]. Beyond polar codes, we have recently shown how to extend the standard classical 'belief propagation' decoding algorithm to the quantum domain in specific instances [9], and how to employ efficient input 'constellations' for classical Gaussian channels to construct similarly efficient quantum codes for quantum Gaussian channels [10].
References
- Marco Tomamichel, Mario Berta and Joseph M. Renes. Quantum coding with finite resources. Nat. Commun. 7, 11419 (2016). external page doi: 10.1038/ncomms11419
- Dina Abdelhadi and Joseph M. Renes. On the second-order asymptotics of the partially smoothed conditional min-entropy & application to quantum compression. external page arxiv:1905.08268
- Joseph M. Renes. Duality of channels and codes. IEEE Trans. Inf. Theory 64, 577 (2018). external page doi: 10.1109/TIT.2017.2754921 external page arxiv:1701.05583
- Joseph M. Renes and Jean-Christian Boileau. Conjectured strong complementary information tradeoff. Phys. Rev. Lett. 103, 020402 (2009). external page doi: 10.1103/PhysRevLett.103.020402 external page arxiv:0806.3984
- Mario Berta, Matthias Christandl, Roger Colbeck, Joseph M. Renes and Renato Renner. The uncertainty principle in the presence of quantum memory. Nat. Phys. 6, 659 (2010). external page doi: 10.1038/nphys1734 external page arxiv:0909.0950
- Joseph M. Renes, Volkher B. Scholz and Stefan Huber. Uncertainty relations: an operational approach to the error-disturbance tradeoff. Quantum 1, 20 (2017). external page doi: 10.22331/q-2017-07-25-20
- Joseph M. Renes, Frederic Dupuis and Renato Renner. Efficient quantum polar coding. Phys. Rev. Lett. 109, 050504 (2012). external page doi: 10.1103/PhysRevLett.109.050504 external page arxiv:1109.3195
- Joseph M. Renes, David Sutter and S. Hamed Hassani. Alignment of polarized sets. IEEE J. Sel. Areas Commun. 34, 224 (2016). external page doi: 10.1109/JSAC.2015.2504271 external page arxiv:1411.7925
- Joseph M. Renes. Belief propagation decoding of quantum channels by passing quantum messages. New J. Phys. 19, 072001 (2017). external page doi: 10.1088/1367-2630/aa7c78
- Felipe Lacerda, Joseph M. Renes and Volkher B. Scholz. Coherent-state constellations and polar codes for thermal Gaussian channels. Phys. Rev. A 95, 062343 (2017). external page doi: 10.1103/PhysRevA.95.062343 external page arxiv:1603.05970